Aliens 優化
Aliens 優化是 DP 優化的一種,先看例題:AI-666 賺多少,雖然這題有 Greedy 的作法,但我們要用 Aliens 優化來做。
先想想看如果沒有交易次數的限制可以怎麼做,令 是到第 個時間點結束時,手上沒有商品的最大獲利,而 是手上有商品的最大獲利, 是時間點 時商品的價格,然後可以很簡單地得到轉移式: 答案就是 ,算這個的同時也可以得到最大獲利需要的最少交易次數是多少。用相似的作法再加上一個維度,就可以算在交易次數限制下的最大獲利了,不過那樣的時間複雜度是 ,所以我們不會這樣做。
令 是做恰 次交易時的最大獲利,雖然我們不能很快地算出 ,但我們可以用 的時間算出 和得到極值發生的 ,也就是最大獲利和需要的交易次數。先知道這件事,待會會用到。
有一個重要的性質是,它是一個凹函數(concave function),凹函數的意思是這個函數的切線斜率也就是差分(我們都在整數上做事)非嚴格遞減,用直覺的方式說明一下就是如果 ,也就是 多做的那次獲利比 多做的那次多,那麼我乾脆把 多做的那次交易換成 多做的那次,所以多出來的獲利一定會越來越少。注意到這樣的說法肯定是不嚴謹的,不過這種性質的證明通常不太容易,因此我們暫且先跳過這個性質的證明。
那麼凹函數可以幹嘛呢?我們要做一件神奇的事情,就是對每次交易多收 元的手續費,令得到的新函數是 ,而 也會是凹函數,因為: 所以就只是 的差分全部減去 而已,差分遞減這件事不會改變。
要計算 和極值發生的 很簡單,只要修改一下轉移式: 同樣可以 算出來。
接下來注意到一件事:對於一個凹函數,它的極值發生點就是第一個 的 ,而「把差分全部減去 」就會改變這個位置,然後我們又可以輕鬆算出來極值和它的位置,還有顯然 越大,極值就會在越左邊的地方,因此我們可以二分搜 (為了實作方便,我們讓這個 是最小的那一個,它會等於 ,讓 剛好變 0),讓極值發生在我們想要的 ,就可以得到 ,把 加回去就是答案了。(這題有一個要特別注意的地方是如果本來極值位置就 ,要直接輸出答案。)
示意圖,藍色是 ,紅色是 ,金色是極值的位置:
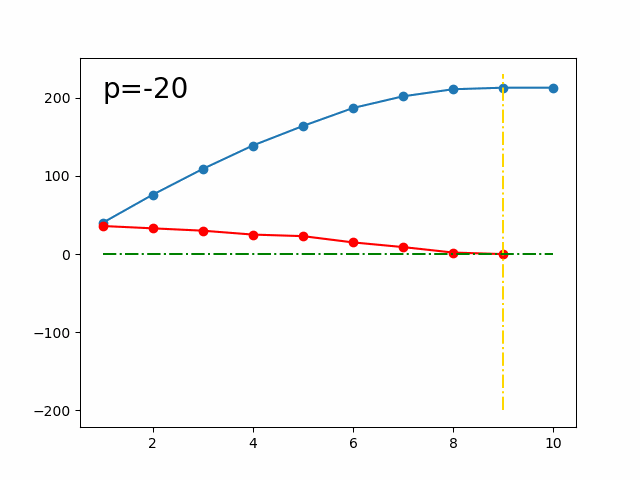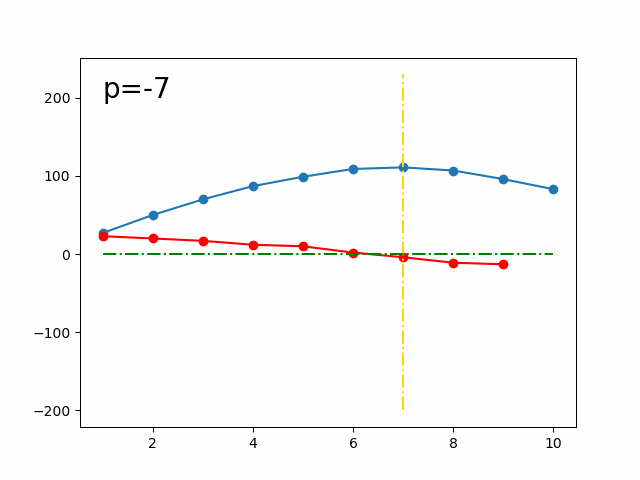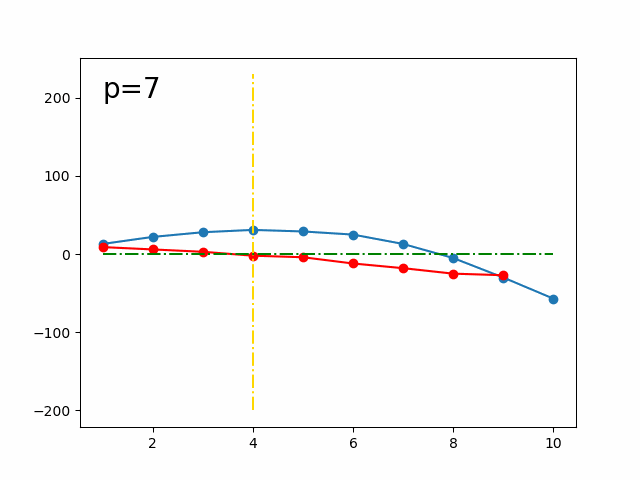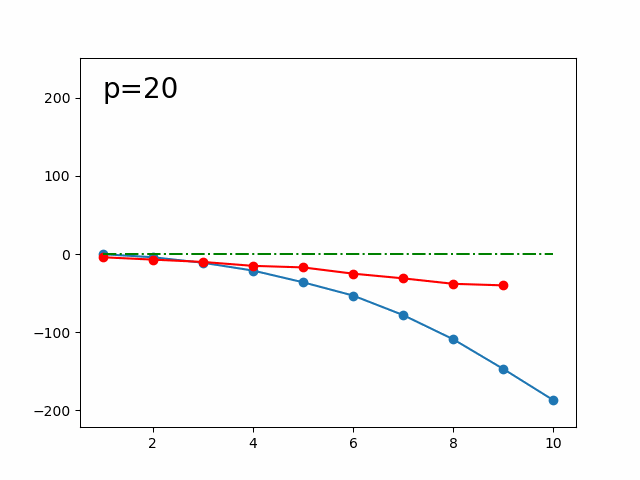
有一個特殊狀況是,因為我們是找「最大獲益需要的最少交易次數」,也就是最左邊的極值位置,而在 ,也就是 等差時, 永遠不會是差分第一個變成 的點,也就不會是最左邊的極值位置。在這個時候,如果直接二分搜的話,會得到一個 滿足 也就是 到 會是一條直線,且 是整條等差的最左邊那個點,可以推得: 也就是 ,因此 ,直接加 也會是好的,結論就是完全不用理會這個狀況。
至於二分搜的上下界呢?因為我們希望最後找到 ,所以這個數字一定要在二分搜的範圍裡,因此二分搜範圍就和差分的範圍一樣。如果不會算的話也可以隨便開一個很大的範圍,反正二分搜很快,TLE 再縮小就好。
時間複雜度是 ,比 好多了。
總結
Aliens 優化就是用這種「移動極值」的想法,來把本來要多開一個維度的事用二分搜做掉。如果用互動題來講,會像是這樣:
有一個凹函數 ,你不知道它長什麼樣子,但是你可以把一個數字 丟進一台機器裡,它會告訴你最大的 是多少,以及讓這個值最大的 為何,求 。
除了凹函數可以用以外,凸函數(差分非嚴格遞增的函數)也可以用 Aliens 優化做,因為它和凹函數同樣有差分具單調性的特性,這樣的題目會變成是求最小值,而極值發生的位置變成第一個 的地方,還有 要換成 (這樣才不用改太多東西 (?)),就是想成它是一個凹函數倒過來就好了。
如果 可能是負數,二分搜的時候注意除法會向零取整。
實作細節
實作就二分搜而已,但有一件特別重要的事情是 是要找最小那一個,在這個時候我們一定會找到 ,剛剛我們都是以這件事為前提做事的,現在來仔細分析一下不這樣做會怎樣。
我們的主要目標是「找到 使得 的極值在 」,在 時,而這個 的範圍可以是 中的任何一個數,在這種時候無論我們找到的 是多少,只要落在這個範圍就會是好的,因為極值一定在 。
而當 就會發生前面有提到的, 不可能是極值位置的狀況發生,這個時候,如果你的二分搜長這樣:
1
2
3
4
5
| while(l < r){
int m = (l + r + 1) / 2;
if(calc(m) >= K) l = m;
else r = m - 1;
}
|
也就是你試圖去找到最大的好的 ,而不是最小的,這樣你其實會得到 ,因為一旦 ,極值位置就會跑到 的左邊去,這樣子 會是 1,且得到的極值位置會是整條等差最右邊那個點,跟我們剛剛想要的 完全不一樣,直接加 回去也會是錯的。
所以二分搜要長這樣才對: 1
2
3
4
5
| while(l < r){
int m = (l + r) / 2;
if(calc(m) <= K) r = m;
else l = m + 1;
}
|
其實也不是一定要這樣,如果你拿上面兩份程式碼各跑一次,會得到兩個 ,假設找最小版是 、找最大版是 ,而得到的極值位置會在整條等差的最左和右邊,假設是 和 ,你可以得到 和 ,反正它們兩個之間等差且 在中間,那就用它們算出 就好: 但是直接加 的作法顯然輕鬆許多,所以就好好找最小的 吧。
AI-666 賺多少的凹函數證明
TODO

