向量

何謂向量

向量（Vector）表示特定的長度和方向，簡單來說，可以想成向量是一個箭頭。例如力、位移都算是向量。

向量可以是任何維度的，也就是說，有二維向量、也有三維向量、一維向量……，然後一個 維向量可以用 個數字來表示，第 個數字表示要往第 個維度的正向走多少距離（如果是負數，就是往負向走），而這個向量可以被看成是一個從起點指向終點的箭頭，舉例來說：

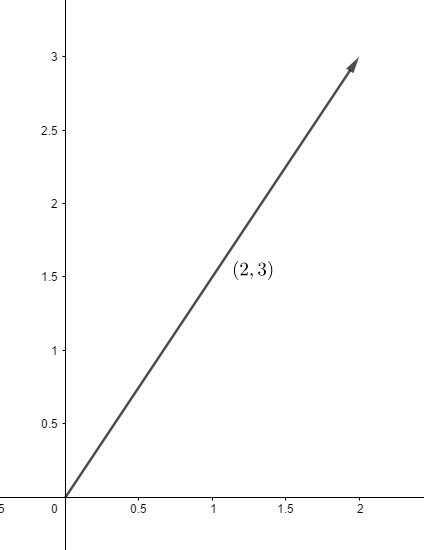這是一個二維向量，它表示向著 軸正向走 ，並向著 軸正向走 ，所以如果從原點開始走，會走到點 。

向量有幾種表示方式，有把數字放在矩陣裡，寫成 或 這種形式的，也有放在 tuple 裡，寫成 的，如果沒有特別需要用到矩陣，通常會用 tuple 來表示。

一個 維向量 的長度可以用畢氏定理來算：

長度為 的向量稱為「零向量」，零向量可以是任意方向的。為了方便，除非特別註明，接下來提到的向量都不包含零向量。

基本符號：

• ，也就是 ，、 是點，表示由 指向 的向量。（注意向量沒有特定的起終點，只能規定它的方向和長度）
• ， 是點，等同於 ， 是原點。
• ，向量 的長度。

基本運算

可以發現到，由原點指向某個點 的向量，就是 ，所以也可以把點想成是向量、也可以把向量想成是點，這會有助於理解接下來的東西。

加減

兩個向量可以相加得到新的向量，就把所有維度的分量分別相加就好：

例如，：

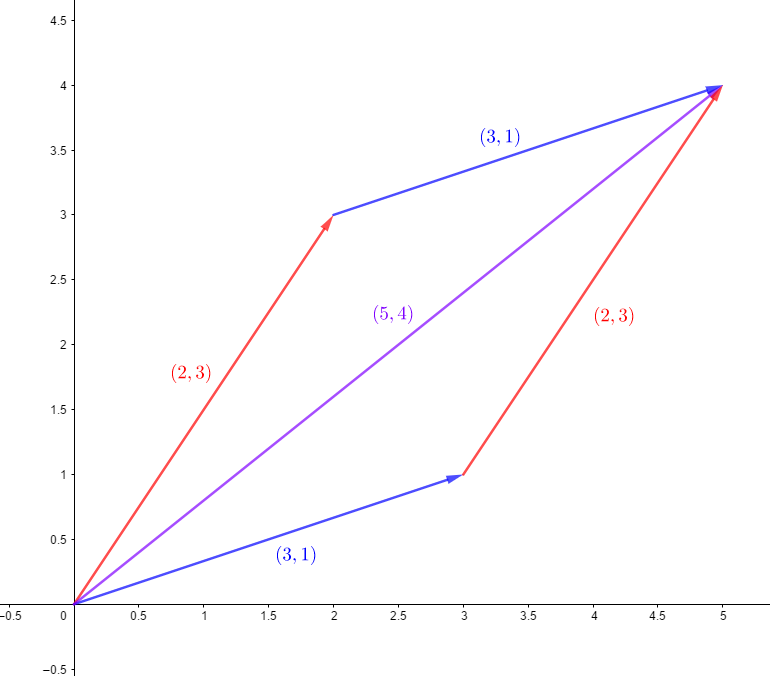
兩個向量相加等同於兩個力的合力，可以發現到這張圖是個平行四邊形。

至於減法，就移項一下就可以暸解要怎麼做了，也可以想成是一個向量加上另一個向量的反向，或者是把兩個向量想成點，，也就是一個從點 指向點 的向量，例如， ：

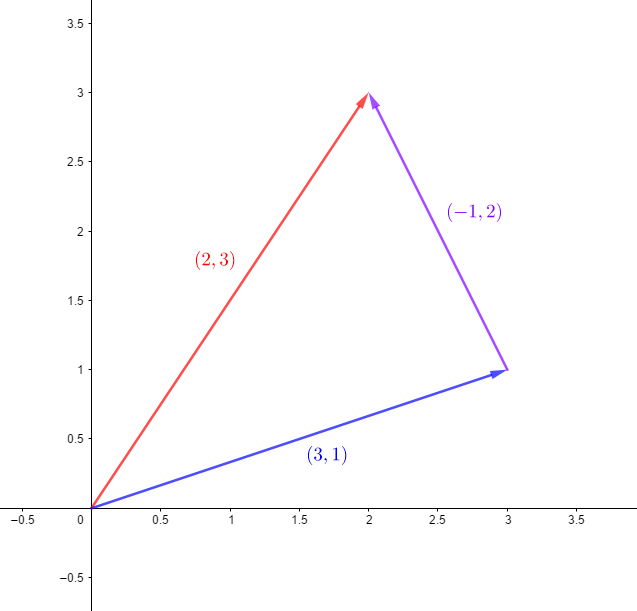
純量乘法

沒有方向的量稱為純量，像是 、、 這些數字都是純量。向量可以乘上一個純量，得到一個新的向量，也就是將這個向量的長度乘上某一個數字，得到一個新的向量，這個動作非常簡單，就把每個維度的分量都乘上這個純量就好：

例如，：

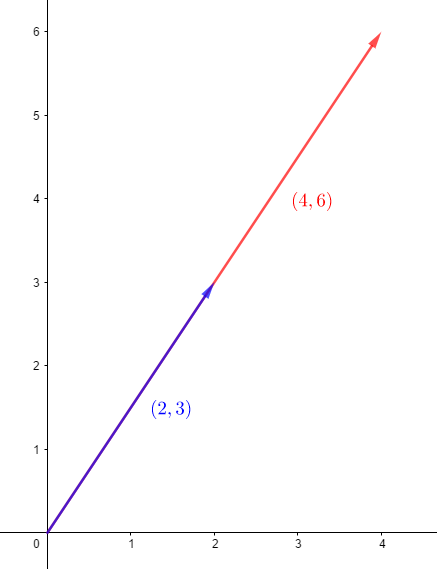
內積（點積）

這是向量特有的運算，兩個夾角是 的 維向量 和 的內積記作 ，結果是一個純量：

其實就是把每一個維度的分量長相乘後相加，例如二維向量 。意義是作一個 在 上垂直投影的向量，然後將這個向量的長和 的長相乘。

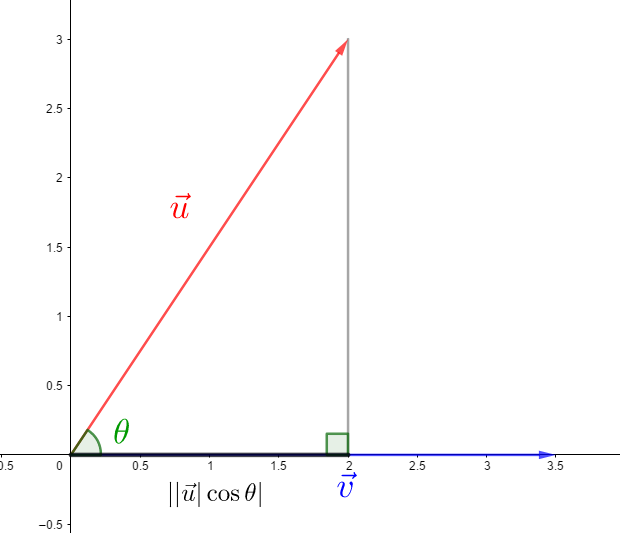
（內積是 再乘上 ，你想要 是裡面那個角還是外面那個角都沒差，畢竟 。如果夾角超過直角，那麼投影會在另一邊，此時 會是負數。）

在力學上的意義是，對一個物體作一個力 ，而物體的位移是 ，則 是 對這個物體所作的功。

既然內積只是多維版本的乘法，那內積也和乘法一樣，有交換律、結合律且對加法有分配律。

接下來針對兩個向量的夾角 大小來討論內積的結果為何：

• 
  顯而易見地，如果作用在一個物體上的力和物體位移方向垂直，那麼這個力對這個物體不作功，且 也確實為 ，因此我們知道，兩個垂直的向量內積是 。

• 
  如果作用在一個物體上的力和物體位移方向相同，那麼這個力作的功等同於力的大小乘上位移距離，同樣 也是 ，因此兩個方向相同的向量 、 的內積是 。

• 
  如果作用在一個物體上的力和物體位移方向相反，那麼這個力作的會是負功，且這個負功的大小等於力的大小乘上位移距離，同樣 是 ，因此兩個方向相反的向量 、 內積是 。

• 
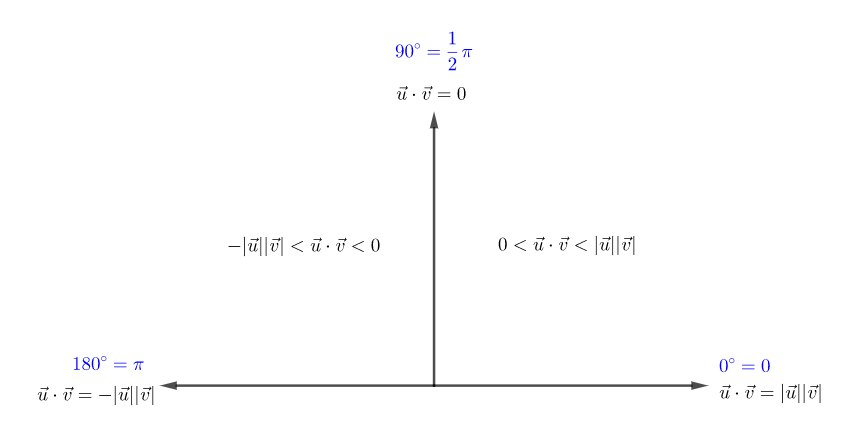
  也就是兩個向量方向在同一邊的時候，顯然如果作用在一個物體上的力和物體位移方向在同一邊，那麼這個力作的會是正功，同樣 的範圍會是 ，因此兩個夾角是 、方向在同一邊的向量 、 內積會是一個正數且 。

• 
  也就是兩個向量方向在不同邊的時候，如果作用在一個物體上的力和物體位移方向在不同邊，那麼這個力作的會是負功，同樣 的範圍會是 ，因此兩個夾角是 、方向在不同邊的向量 、 內積會是一個負數且 。

兩向量在不同夾角時的內積：

兩個長度為 的向量在不同夾角時的內積（ 軸為夾角（弧度）、 軸為內積）：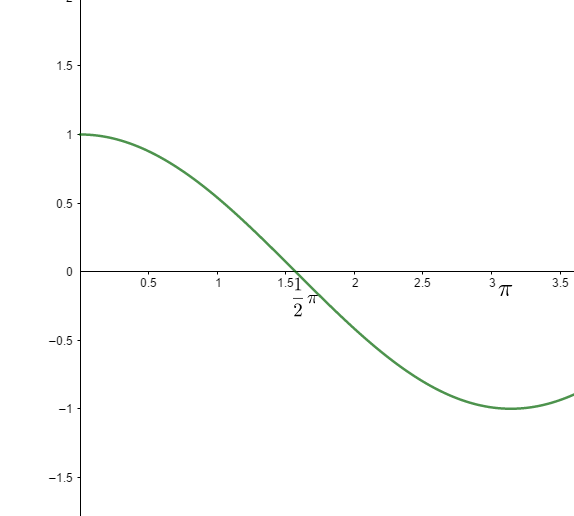

內積常被用來判斷兩個向量是否垂直，也可以用來判斷兩個向量的方向是否在同一邊、是否相同或者相反。

外積（叉積）

向量特有的運算，在定義上，它只能用在三維，兩個三維向量 和 的外積記作 ，是一個新的二維向量 （）：

其中，、、 是三個維度的「基向量」，也就是 、、。外積得到的向量會垂直於 和 構成的平面，且當 和 的夾角是 ，外積得到的向量長度是：

它的長度等同於兩個向量所夾的平行四邊形面積。

至於它的方向，會依據右手定則，右手食指指向 ，中指指向 ，大姆指的方向就會是 的方向。

以上不重要 (?)。二維向量的外積比較常用，但剛剛不是說只能用在三維？你會發現把第三維全部代 ，就會變成：

的部分我們不要管它，把二維外積定義為三維外積的長度（純量），如果三維外積的結果向量向上，那二維外積是正的，否則就是負的，可以得出：

相同地，這個值等同於兩個向量所夾的平行四邊形面積，但它是「有向」的，如果 轉向 是逆時針，那會是正的，反之就會是負的（這邊的轉指往較近那邊轉），至於夾角 是指 往逆時針轉到 的角度。

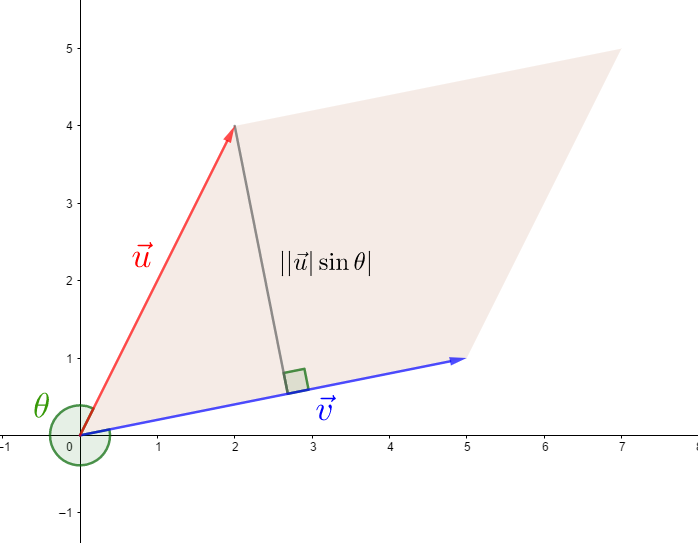
外積沒有交換律，也就是說 ，但它滿足「負交換律」，也就是 ，因為：

外積沒有結合律（甚至二維的外積算出來也不是向量），但對加法有分配律。

接下來我們針對各種夾角 討論它的值：

• 
  這樣兩個向量會夾一個長方形，且 ，因此兩個夾角為直角的向量 、 外積為 。

• 
  這樣兩個向量會夾一個長方形，且 ，但 轉向 是順時針，因此。

• 
  兩個向量同向，那麼它們夾的平行四邊形面積為 ，且 ，因此此時外積值為 。

• 
  兩個向量反向，此時它們夾的平行四邊形面積也為 ，且 ，因此此時外積值為 。

• 
  往 轉是逆時針，且 ，則 。除非 ，不然 ，則 。

• 
  往 轉是順時針，且 ，則 。除非 ，不然 ，則 。

兩向量在不同夾角時的外積：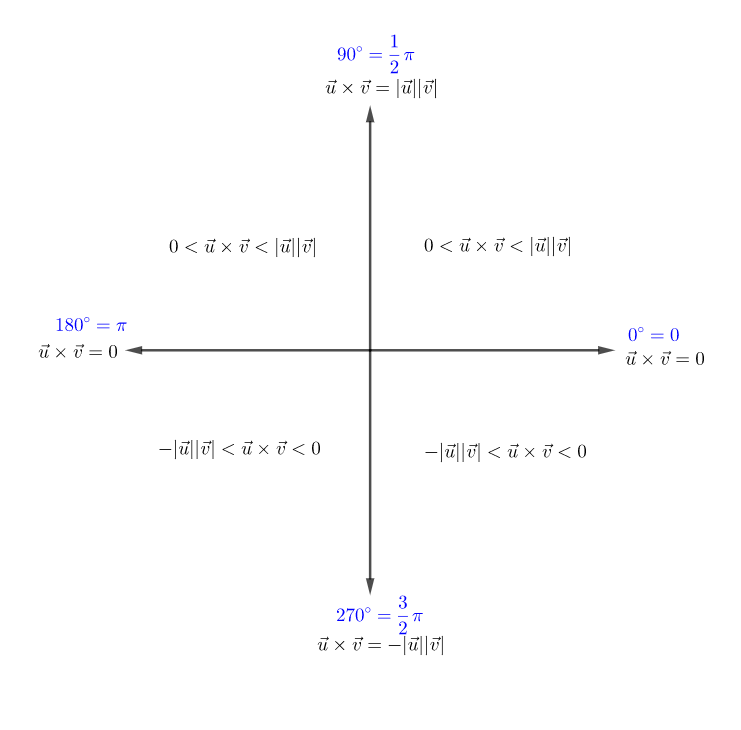

兩個長度為 的向量在不同夾角時的外積（ 軸為夾角（弧度）、 軸為外積）：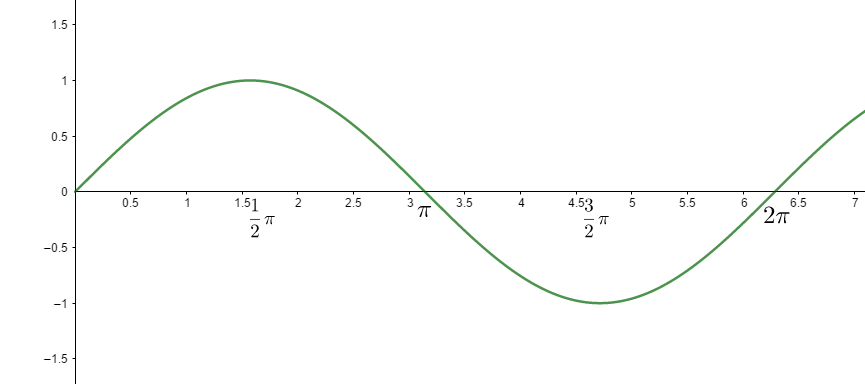

實作

有些人會把向量（或點）做成一個 class，不過我自己是習慣直接用 pair，然後再做運算子重載。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

#define F first
#define S second
#define mp make_pair

template<typename T>
pair<T, T> operator+(pair<T, T> a, pair<T, T> b){
    return mp(a.F + b.F, a.S + b.S);
}

template<typename T>
pair<T, T> operator-(pair<T, T> a, pair<T, T> b){
    return mp(a.F - b.F, a.S - b.S);
}

template<typename T>
pair<T, T> operator*(pair<T, T> a, T b){
    return mp(a.F * b, a.S * b);
}

template<typename T>
pair<T, T> operator/(pair<T, T> a, T b){
    return mp(a.F / b, a.S / b);
}

template<typename T>
T dot(pair<T, T> a, pair<T, T> b){
    return a.F * b.F + a.S * b.S;
}

template<typename T>
T cross(pair<T, T> a, pair<T, T> b){
    return a.F * b.S - a.S * b.F;
}

template<typename T>
T abs2(pair<T, T> a){
    return a.F * a.F + a.S * a.S;
}