樹狀數組

有一個序列 ，一開始都是 0，有 筆操作，每筆操作都是以下其中一種：

1. 把 加上
2. 詢問 區間和

雖然帶修改前綴和也可以用線段樹來做，不過有一個更適合用在前綴和的可修改結構——樹狀數組／二元索引樹（Binary Indexed Tree，簡稱 BIT）。BIT 的常數小，實作也更簡單。

BIT 的空間只要 ，比線段樹的 小，只需要用一個一維陣列就可以儲存一棵 BIT 了。

BIT 的每一個位置表示的值根據它的位置編號而定， 定義為：以 為結尾，長度為 的區間和，也就是 這個範圍的和， 指的是把 轉成二進位後，把最低位的 以外的 都變成 ，例如

所以說， 就是 這個區間的和。

要得到 的方法是 x&-x，也就是把它和它的相反數取 bitwise and，因為 -x 會是 x 的補數加 ，x 在最低位的是 的位元會變為 ，右邊的 在取補數後會變為 ，加上 之後，這些又會變為 ，而本來是最低位的 的地方也會變為 ，但在左邊的每一個位元都會和本來不同，因為取 bitwise and 後，就可以得到 。

節點 代表的是一個空區間，而節點 的區間只包含 ，因此，序列的索引應該要從 開始。

那麼 BIT 畫成樹是什麼樣子？其實它並不是二元樹，binary 指的是二進位。

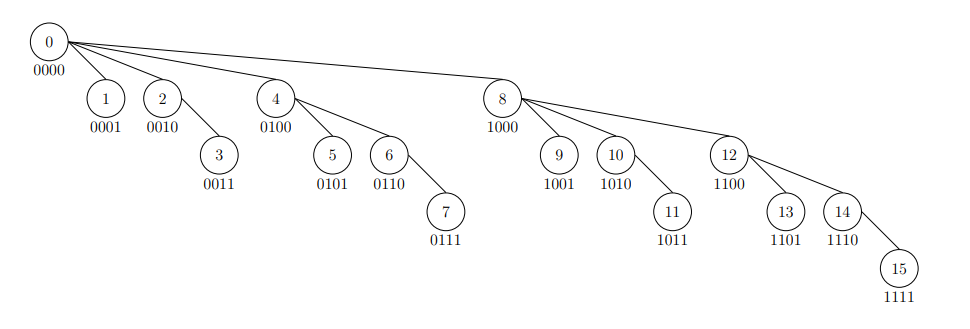
• 節點 的父節點是 。
• 節點 的深度與 是 的位元數相同。
• 節點 的右兄弟節點（如果有的話）是 。

節點 就是根節點，然後按照上述規則，可以畫出一棵樹。仔細觀察一下，會發現每個節點代表的區間有這些性質：

• 節點 的父節點是 ，則節點 的區間是 ，因為 。
• 節點 的區間包含它所有左兄弟節點的區間，因為它們的父節點都一樣，所以它們區間的起點都一樣，但 的結束點較後面。
• 節點 的區間包含所有左兄弟節點 的子孫節點的區間，因為 子孫節點區間必在 和 之間，而 的區間肯定包含這段。

在知道這些性質後，就可以來討論怎麼處理詢問了。

單點修改

如果現在要修改一個位置 ，那要找到所有區間包含這個位置的節點，第一個這樣的節點是 ，接下來，它的所有右兄弟節點都包含這裡，用 可以得到右兄弟節點，而其父節點的右兄弟節點也包含這個點，若 最右邊的兄弟節點是 ，那其父節點的右兄弟會是 。

所以只要一直把 加上 ，就可以得到它和它祖先的所有右兄弟節點，修改這些節點的答案就好了。

實作相當簡單：

1
2
3
4
5
6

void modify(int pos, int x){ // 把 pos 改成 x
    // n 是序列大小
    for(; pos <= n; pos += lowbit(pos)){
        修改節點 pos 的答案;
    }
}

可以發現 會不斷增加，所以複雜度是 。

前綴查詢

要查詢以 為結尾的前綴，就應該找到幾段不重疊，且聯集恰好是所求前綴的區間。

區間以 為結尾的節點是 ，而節點 的區間剛好緊接在它的父節點之後，它的父節點是 ，所以只要找到 和它所有祖先節點，這些區間聯集起來就是我們想要的前綴。

實作也非常簡單：

1
2
3
4
5
6
7

type query(int pos){
    type ans;
    for(; pos > 0; pos -= lowbit(pos)){
        更新ans;
    }
    return ans;
}

同樣地， 會不斷增加，因此複雜度是 。

建構

如果有初始值的話，就把每一個元素分別 modify 就好了，複雜度是 。

應用

BIT 最基礎的應用就是拿來算前綴和，因為和是一種「可返回」的東西，減去本來的值在加上新的值就可以得到新的和，而有了前綴和就也可以算區間和了，且它比線段樹好寫很多。

BIT 前綴和和差分結合使用，就可以做到 區間修改、 單點查詢。

BIT 也可以區間修改、區間查詢前綴和。先算出要做的序列 的差分序列 ， 的索引從 開始，然後我們可以得出 這個區間的和是：

然後可以把它化成：

那麼只要用兩個 BIT，一個維護 、另一個維護 ，這樣就可以做區間修改、區間求和了。

至於 BIT 可不可以做最大最小值這種「不可返回」的操作呢？如果在求最大值的數字時，把其中一個位置改小，那麼是沒辦法單靠被修改的位置就得出新的最大值的，因此如果要用 BIT 做最大值，數字只能被改大，做最小值，數字只能被改小。

練習題

• ZeroJudge d799 - 區間加值、詢問區間和
• TIOJ 1175 - LIS
• TIOJ 1869 - 二維 BIT
• TIOJ 1080 - 逆序數對