凸包

你有一大堆點，然後你要找出一個可以圍住這些點且面積最小的凸多邊形，這個凸多邊形稱為凸包。

顯而易見，如果要面積最小，那凸包的頂點勢必得是這一大堆點的其中幾個點，你也可以想成是用一條橡皮筋把這些點圈起來。

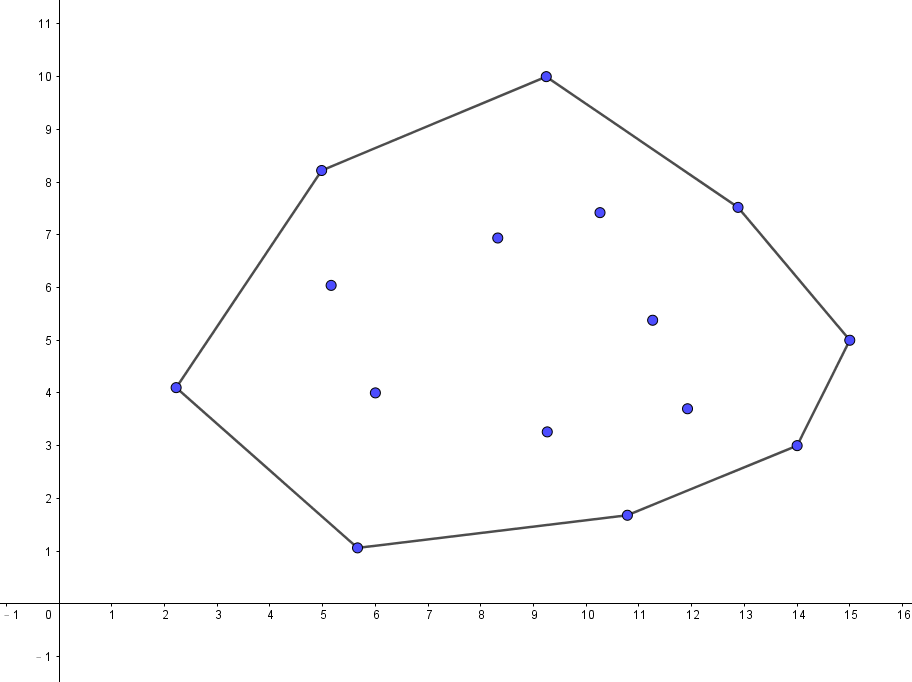
那麼，如何有效率地把凸包蓋出來呢？

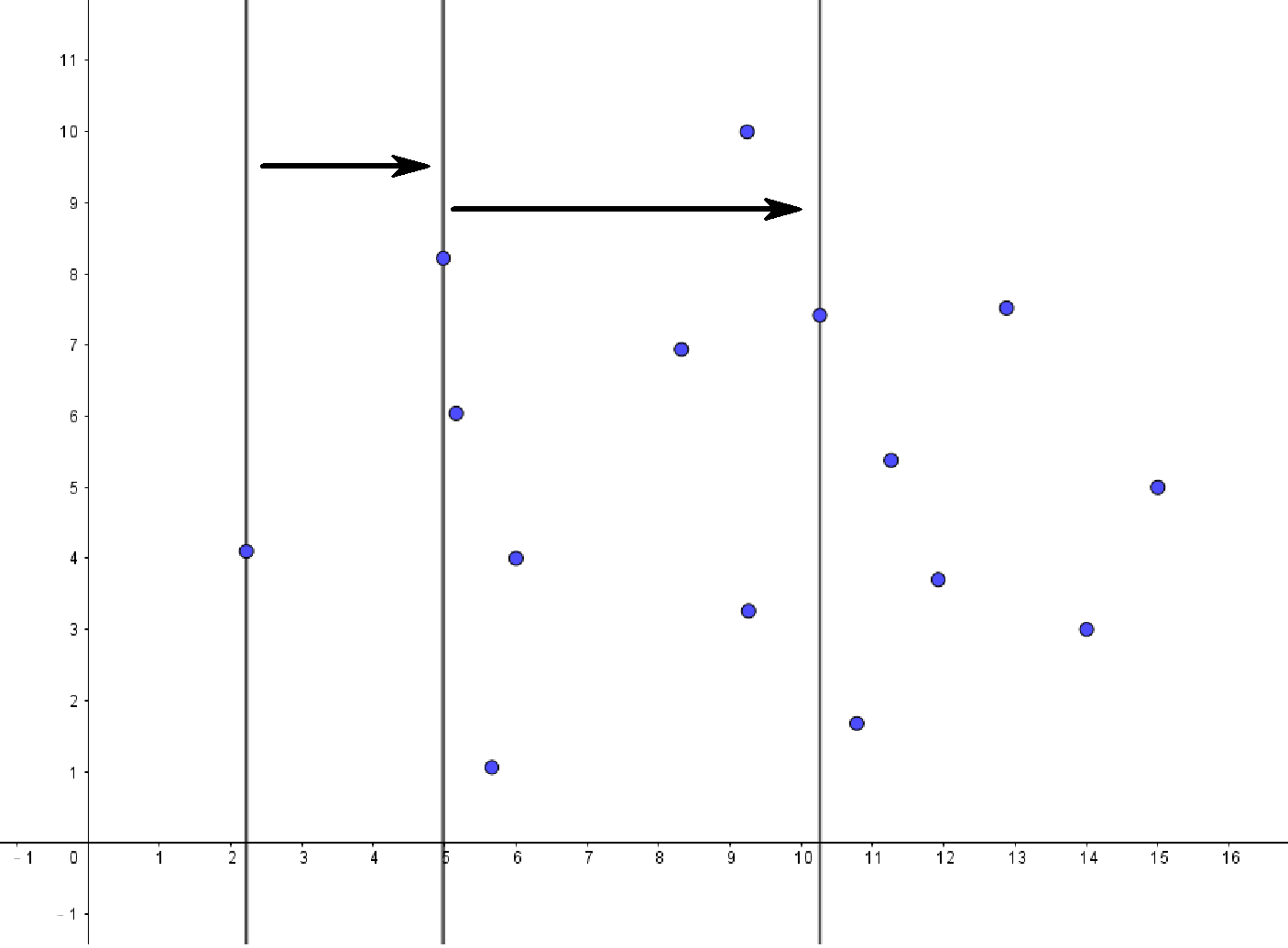
先把各個點按座標由小到大排序，座標相同則再按座標由小到大排序，排序之後的點順序會是由左至右、由上至下，這樣一來我們就可以按這個順序遍歷這些點，這種往固定方向掃描的方式，稱為掃描線。

知道點的左右上下關係可以幹嘛？

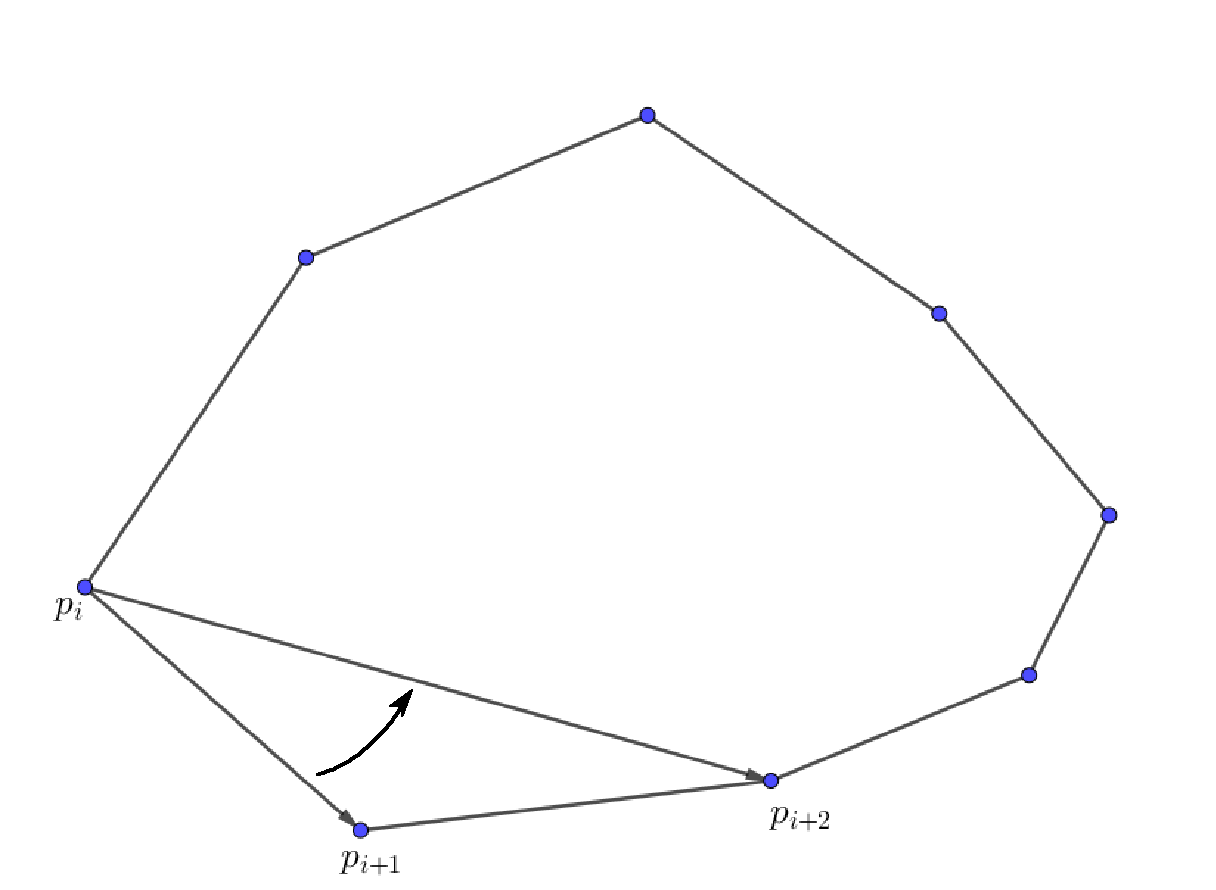
先討論一件事情：有一個凸多邊形，它的頂點已經按逆時針順序排好了，依序是，那麼和與的關係會是什麼（令）？既然是凸多邊形，那麼它的邊應該要是一直往同個方向轉彎的，而如果將邊逆時針排序，這個邊的斜率也應該是一直往逆時針方向轉彎，顯然點也會是這樣，因此：

再來，我們把凸包分成上下兩部分：上凸包和下凸包，以極左和極右點分割，如果極左點或極右點有兩個（最多只會有兩個），上面那個屬於上凸包，下面那個屬於下凸包，否則極左點必屬於下凸包，極右點必屬於上凸包。

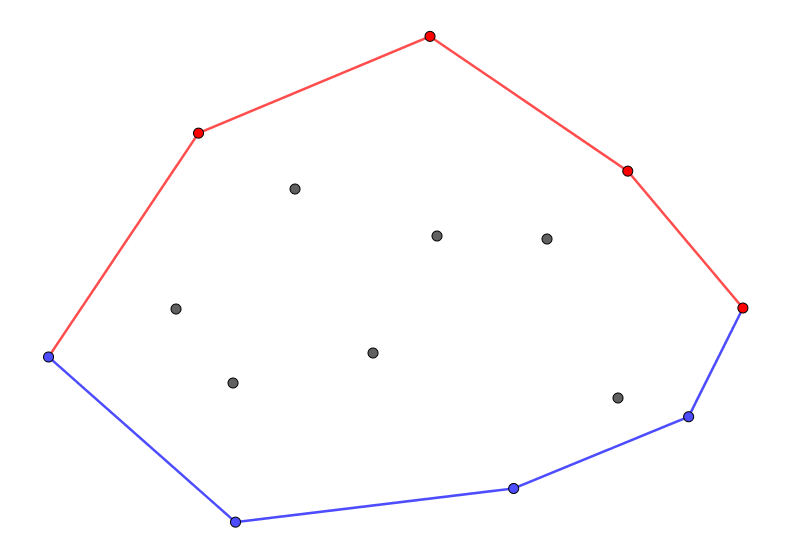
顯然，上或下凸包中不會有座標相同的頂點，因此在上或下凸包中，每個頂點都能分別出左右的關係，並且你會發現，如果把點按逆時針排序，在下凸包中的點也是由左而右排序的、在上凸包的點也是由右而左排序的。

這樣一來左右關係就有用了，先用由左而右的掃描線把下凸包做出來，再用由右而左的掃描線把上凸包做出來，就可以得到整個凸包。

這整個流程可以用一個 stack 來實作，在處理一個點的時候，我們嘗試把它加進凸包裡，此時這個點是，堆頂的點是，堆頂再往下一個點是，把這些點代入剛剛的式子，符合條件或者 stack 大小小於時就停止，否則就把堆頂 pop，然後繼續重複，結束之後就把目前處理中的點放入堆頂。

在做下凸包的時候，先從最左邊且最下面的點開始做上述動作，做到最後，堆頂的點應該會是最右邊且最上面的點，把它 pop 掉，因為它應該屬於上凸包；做上凸包的時候，從最右邊且最上面的點開始做，最後堆頂會是最左且最下的點，把它 pop 掉後，這兩個接起來就是完整的凸包。

因為要用到堆頂往下一個點，所以 stack 用 vector 來實作。

#include <bits/stdc++.h>

#define mp(a, b) make_pair(a, b)
#define pb(a) push_back(a)
#define F first
#define S second

using namespace std;

template<typename T>
pair<T, T> operator-(pair<T, T> a, pair<T, T> b){
    return mp(a.F - b.F, a.S - b.S);
}

template<typename T>
T cross(pair<T, T> a, pair<T, T> b){
    return a.F * b.S - a.S * b.F;
}

template<typename T>
vector<pair<T, T>> getConvexHull(vector<pair<T, T>>& pnts){

    int n = pnts.size();
    sort(pnts.begin(), pnts.end());

    vector<pair<T, T>> hull;

    for(int i = 0; i < 2; i++){
        int t = hull.size();
        for(pair<T, T> pnt : pnts){
            while(hull.size() - t >= 2 && cross(hull.back() - hull[hull.size() - 2], pnt - hull[hull.size() - 2]) <= 0)
                hull.pop_back();
            hull.pb(pnt);
        }
        hull.pop_back();
        reverse(pnts.begin(), pnts.end());
    }

    return hull;
}

這個演算法叫 Andrew's monotone chain，另一種比較常聽到的凸包演算法是 Graham's scan，有興趣可以自己查。

練習題

TIOJ 1178 - 給一堆點，求凸包的頂點數量
ZeroJudge a871 - 求凸多邊形面積（點不一定照順序）
ZeroJudge d546 - 求多邊形面積和凸包面積差
TIOJ 1280 - 給你一堆點，求所有點對連成的直線所能圍出的最大面積

旋轉卡尺

用旋轉兩條平行線、夾住一堆點，看在線上的點是哪些，就叫旋轉卡尺。

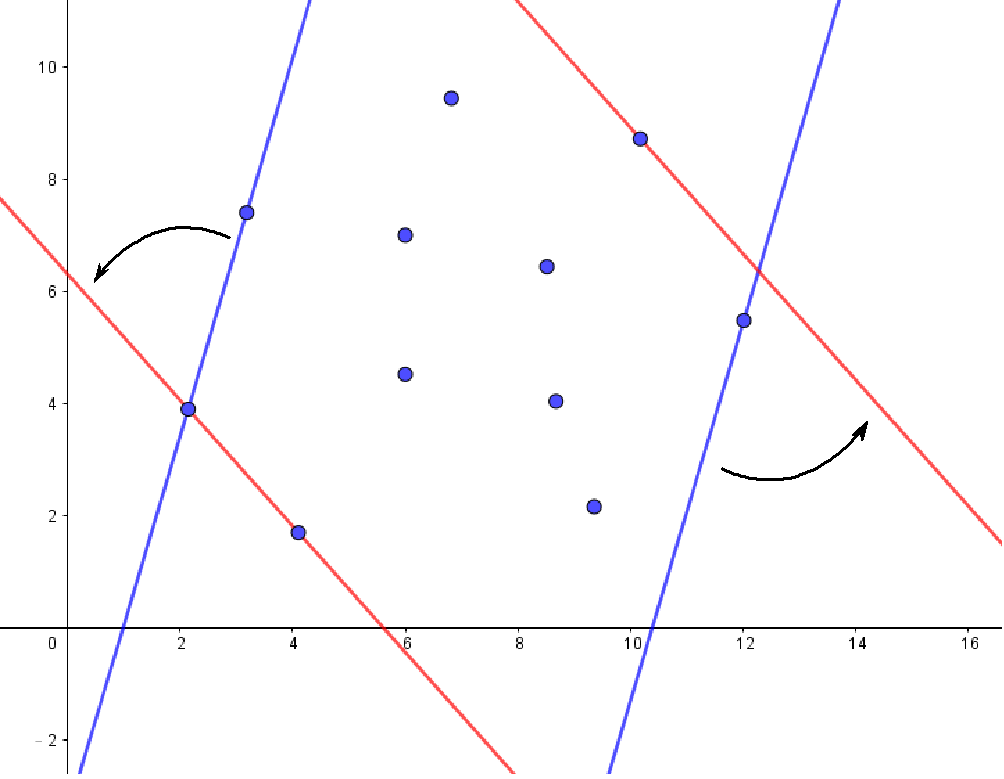
旋轉線、夾點感覺很麻煩，是不是要用到什麼角度的東西啊？其實不用，先來分析一下問題，用兩條平行線夾一堆點，那麼平行線只會碰到凸包上的點而已，所以不在凸包上的點都可以先忽略：

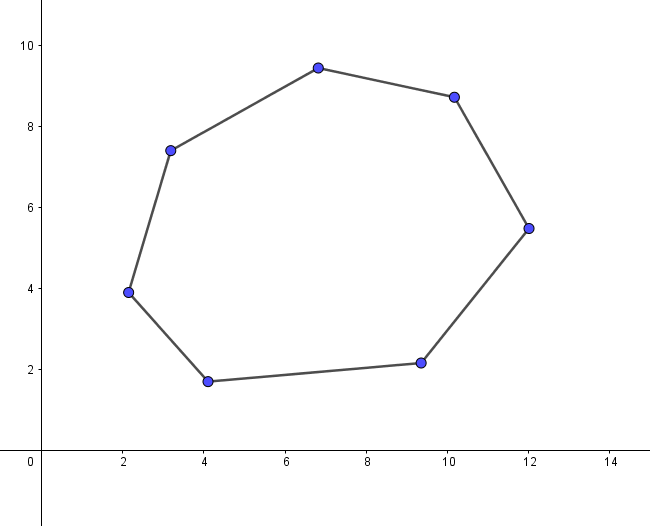
過一個點的直線有很多條，但是過一個線段的直線只有一條，所以先枚舉線段，再去找和它平行的直線應該會夾到哪個點，這樣問題就簡單多了。要找平行線會碰到哪個點，顯然離線段最遠的點就是了。

不過算距離是另一個問題，聽起來也很麻煩，但其實很簡單。一個點距離一條直線的距離，等同於過該點在直線上作垂線段的長，而一開始選定的線段作為底、垂線段長作為高，那麼就可以得到一個平行四邊形面積了，且底的長是固定的，只要枚舉最遠點，就等同於枚舉高，而得出面積最大的，就是我們要的最遠點了。

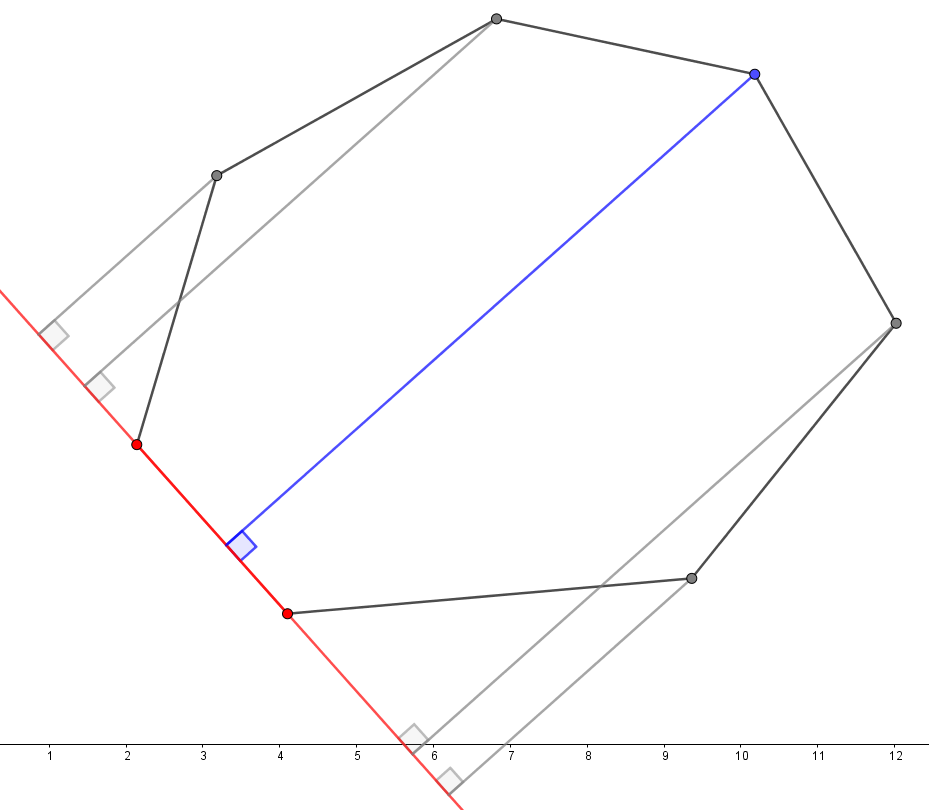
上圖中，選定兩個紅色點所連成的線段為底，然後枚舉各個頂點取高，得出藍色垂線是最長的，因此藍色點就是距離紅色線段最遠的點。

這就是旋轉卡尺的基礎應用——最遠點對，找到距離每一線段最遠的點，再取該點與線段兩端點的距離取最大值，這樣就可以得出所有點中最遠的點對為何。

硬要這麼做的方式，時間複雜度是，是凸包上點的數量（不計蓋凸包的複雜度），枚舉線段是，再枚舉一個點要再乘上。

這不夠快，我們需要更有效率的方式。

仔細觀察一下，點和線段的距離有一個規律——先漸大，到一個最大值，再漸小：

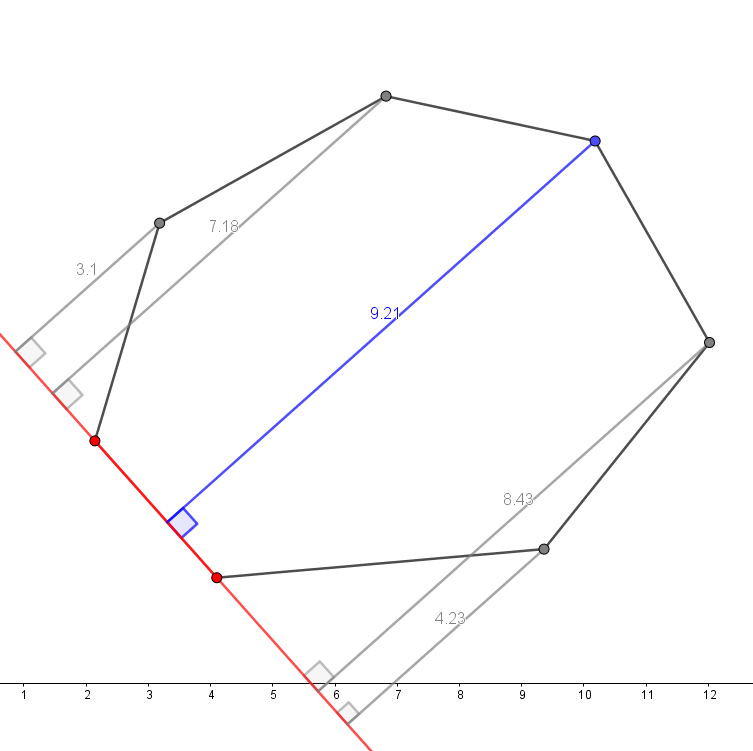
我們發現它會呈現一個單峰函數，也就是一個先遞增、再遞減的函數，這樣我們就可以用三分搜找到最高點了，這樣三分搜一次的複雜度是，再乘上點的數量，就是。

這樣子還是不夠快，前面提到旋轉卡尺是「旋轉兩條平行線」，剛剛的動作都是旋轉其中一條，再去搜尋另一條，那我們可不可以在旋轉其中一條的同時，把另一條一起旋轉？答案是：可以。

（以下的轉都是指往同一個方向轉）
先找到距離第一條邊最遠的點，過前者的線稱為第一條平行線，過後者的稱為第二條平行線，接下來我們轉動第一條平行線，也就是把它轉到第二條線段上，而第二條平行線不要動，會發現，第一條平行線離第二條平行線那個點近了一些，接著再轉第二條平行線，也就是把它轉到下一個點上，那麼距離會變遠。

也就是，可以在不重新來過的情況下，找到單峰函數的最高點，會發現這樣就是把兩條平行線繞一圈，因此這樣的複雜度是。

最大三角形

給你一堆點，請找出這些點所能構成的面積最大的三角形。

用類似最遠點對的想法來想，先枚舉兩個頂點，然後再用旋轉卡尺去找第三個頂點。首先，先枚舉第一個點，然後在枚舉第二個點的同時，第三個點可以跟著往下轉，這樣就可以解決這件事。

練習題

ZeroJudge b288 - 最大三角形
TIOJ 1105 - 最遠點對

WiwiHo

2024-03-31