Sparse Table
有一個序列
,有 筆詢問,每筆詢問求 的區間最大值。
如果是要求區間和的話,前綴和在經過
如果算出每一個
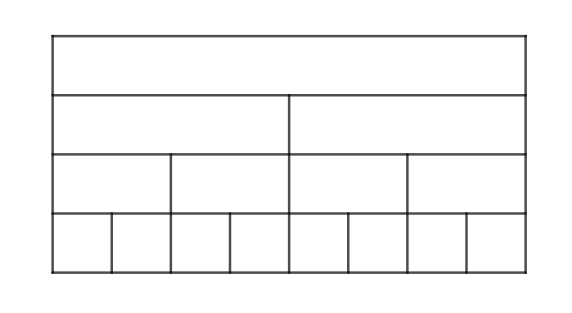
(
令
長度
當
最後,當我們要求
這樣一來,我們就可以先預處理整個
因為同一個元素會被很多區間包含,所以 Sparse Table 不能做修改。
練習題
- ZeroJudge d539 - 區間詢問最大值
- TIOJ 1338 - 詢問區間內有沒有一個數字整除區間內全部的數字
有一個序列
,有 筆詢問,每筆詢問求 的區間最大值。
如果是要求區間和的話,前綴和在經過
如果算出每一個

(
令
長度
當
最後,當我們要求
這樣一來,我們就可以先預處理整個
因為同一個元素會被很多區間包含,所以 Sparse Table 不能做修改。